Education

Stanford University
Sep. 2020 - Now, Computer Science PhD
Stanford University
Sep. 2016 - Jun. 2020, Mathematics B.S.
• With distinction
Selected Publications
-
On Distillation of Guided Diffusion Models (CVPR 2023, Award candidate)
Chenlin Meng, Robin Rombach, Ruiqi Gao, Diederik P. Kingma, Stefano Ermon, Jonathan Ho, and Tim Salimans
Diffusion models typlically requires tens to hundreds of model evalutions
to generate one image. Using our approach, we only need 2-4 evalutions, drastically reducing the sampling cost. Our approach is also hightly effective for video generation and is used in Imagen Video.
[Paper | Code (Coming soon)]

-
SDEdit: Image Synthesis and Editing with Stochastic Differential Equations (ICLR 2022)
Chenlin Meng, Yutong He, Yang Song, Jiaming Song, Jiajun Wu, Jun-Yan Zhu, and Stefano Ermon
SDEdit is an effective image editing and style-transfer method. It has
been broadly used in state-of-the-art generative AI frameworks including Stable Diffusion (see here) and GLIDE. It is more commonly known as "Image2Image" for Stable Diffusion.
[Paper | Project Page | Colab | Code]

-
Denoising Diffusion Implicit Models (ICLR 2021)
Jiaming Song, Chenlin Meng and Stefano Ermon
Diffusion models typlically requires hundreds of denoising steps
to generate one image, which is expensive and often infeasible in real-world settings. This paper is one of the earliest works to reduce the denoising steps of diffusion models from >1000 to <100.
It has been widely used in Stable Diffusion, DALL-E 2, Imagen, GLIDE, eDiff-I and many others.
[Paper | Code]

-
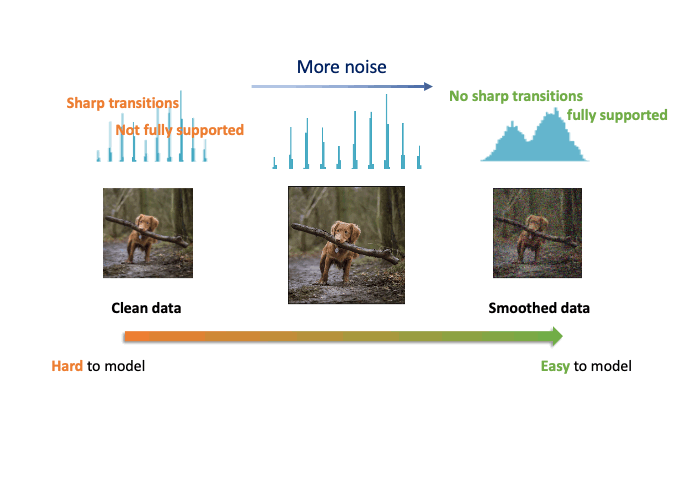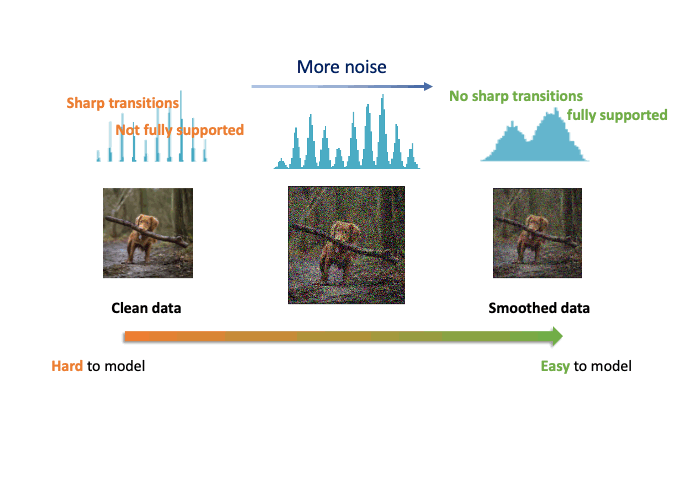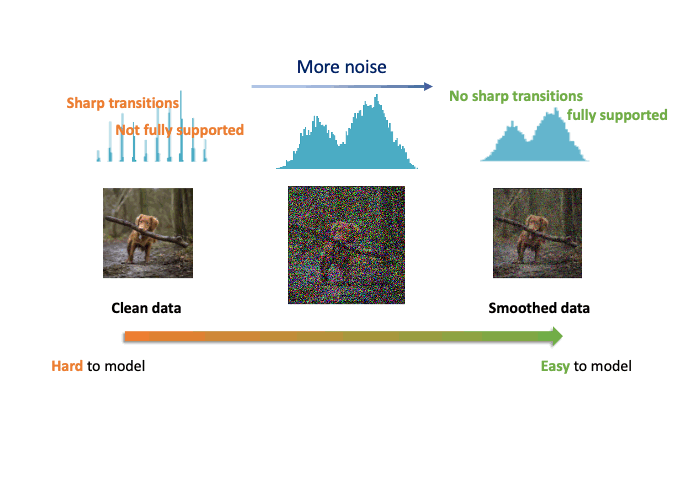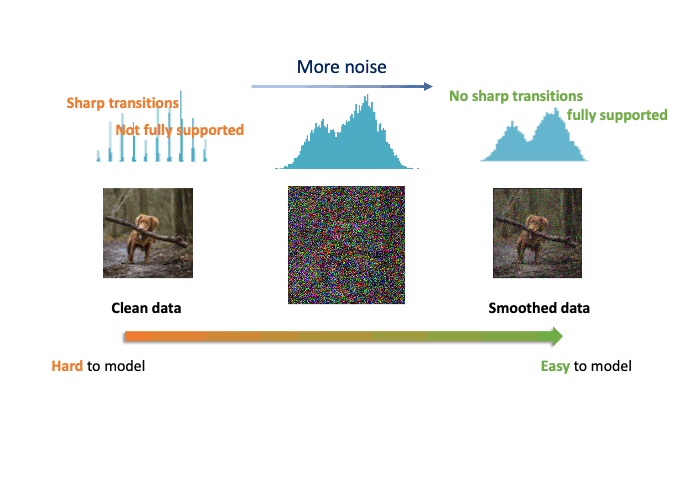
Improved Autoregressive Modeling with Distribution Smoothing
(ICLR 2021) Oral Presentation [top: 1.8%]
Chenlin Meng, Jiaming Song, Yang Song, Shengjia Zhao, and Stefano Ermon
While autoregressive models excel at image compression, their sample quality is often lacking. We propose a denoising-based approach to drastically improve the performance of autoregressive models on image generation tasks.
[Paper | Project Page | Code]
-
D2C: Diffusion-Denoising Models for Few-shot Conditional Generation (NeurIPS 2021)
Abhishek Sinha, Jiaming Song, Chenlin Meng, and Stefano Ermon
D2C uses a learned diffusion-based prior over the latent representations to improve generation and contrastive self-supervised learning to improve representation quality. D2C can adapt to novel generation tasks conditioned on labels or manipulation constraints, by learning from as few as 100 labeled examples.
[Paper | Project Page | Code]

-
Concrete Score Matching: Generalized Score Matching for Discrete Data (NeurIPS 2022)
Chenlin Meng*, Kristy Choi*, Jiaming Song, and Stefano Ermon
Representing probability distributions by the gradient of their density functions (e.g., diffusion model) has proven effective in modeling a wide range of continuous data modalities.
However, this representation is not applicable in discrete domains where the gradient is undefined.
To this end, we propose an analogous score function called the "Concrete score", a generalization of the (Stein) score for discrete settings.
[Paper | Code (Coming soon)]

Publications
- On Distillation of Guided Diffusion Models (CVPR 2023, Award candidate) Chenlin Meng, Ruiqi Gao, Diederik P. Kingma, Stefano Ermon, Jonathan Ho, and Tim Salimans [Paper | Code (Coming soon)]
- Concrete Score Matching: Generalized Score Matching for Discrete Data (NeurIPS 2022) Chenlin Meng*, Kristy Choi*, Jiaming Song, and Stefano Ermon [Paper | Code (Coming soon)]
- SatMAE: Pre-training Transformers for Temporal and Multi-Spectral Satellite Imagery (NeurIPS 2022) Yezhen Cong*, Samar Khanna*, Chenlin Meng, Patrick Liu, Erik Rozi, Yutong He, Marshall Burke, David Lobell, Stefano Ermon [Paper | Project Page | Code]
- Efficient Spatially Sparse Inference for Conditional GANs and Diffusion Models (NeurIPS 2022) Muyang Li, Ji Lin, Chenlin Meng, Stefano Ermon, Song Han, Jun-Yan Zhu [Paper | Project Page | Code]
- Self-Similarity Priors: Neural Collages as Differentiable Fractal Representations (NeurIPS 2022) Michael Poli*, Winnie Xu*, Stefano Massaroli*, Chenlin Meng, Kuno Kim, Stefano Ermon [Paper | Project Page | Code]
- Generalizing Bayesian Optimization with Decision-theoretic Entropies (NeurIPS 2022) Willie Neiswanger*, Lantao Yu*, Shengjia Zhao, Chenlin Meng, Stefano Ermon [Paper | Code (Coming soon)]
- ButterflyFlow: Building Invertible Layers with Butterfly Matrices (ICML 2022) Chenlin Meng*, Linqi Zhou*, Kristy Choi*, and Stefano Ermon [Paper | Code (Coming soon)]
- SDEdit: Image Synthesis and Editing with Stochastic Differential Equations (ICLR 2022) Chenlin Meng, Yutong He, Yang Song, Jiaming Song, Jiajun Wu, Jun-Yan Zhu, and Stefano Ermon [Paper | Project Page | Colab | Code]
- Density Ratio Estimation via Infinitesimal Classification (AISTATS 2022) Oral Presentation [top: 2.6%] Kristy Choi*, Chenlin Meng*, Yang Song, and Stefano Ermon [Paper | Code]
- IS-COUNT: Large-scale Object Counting from Satellite Images with Covariate-based Importance Sampling (AAAI 2022) Oral Presentation Chenlin Meng*, Enci Liu*, Willie Neiswanger, Jiaming Song, Marshall Burke, David B. Lobell, and Stefano Ermon [Paper | Project Page | Code]
- SustainBench: Benchmarks for Monitoring the Sustainable Development Goals with Machine Learning (NeurIPS 2021, Datasets and Benchmarks Track) Christopher Yeh*, Chenlin Meng*, Sherrie Wang*, Anne Driscoll, Erik Rozi, Patrick Liu, Jihyeon Lee, Marshall Burke, David B. Lobell, and Stefano Ermon [Paper | Project Page | Code]
- Estimating High Order Gradients of the Data Distribution by Denoising (NeurIPS 2021) Chenlin Meng, Yang Song, Wenzhe Li, and Stefano Ermon [Paper | Code]
- D2C: Diffusion-Denoising Models for Few-shot Conditional Generation (NeurIPS 2021) Abhishek Sinha, Jiaming Song, Chenlin Meng, and Stefano Ermon [Paper | Project Page | Code]
- Spatial-Temporal Super-Resolution of Satellite Imagery via Conditional Pixel Synthesis (NeurIPS 2021) Yutong He, Dingjie Wang, Nicholas Lai, William Zhang, Chenlin Meng, Marshall Burke, David B. Lobell, and Stefano Ermon [Paper | Project Page]
- Geography-Aware Self-Supervised Learning (ICCV 2021) Kumar Ayush*, Burak Uzkent*, Chenlin Meng*, Kumar Tanmay, Marshall Burke, David Lobell, and Stefano Ermon [Paper | Code | Project Page]
- Accelerating Feedforward Computation via Parallel Nonlinear Equation Solving (ICML 2021) Yang Song, Chenlin Meng, Renjie Liao, and Stefano Ermon [Paper | Code]
- Improved Autoregressive Modeling with Distribution Smoothing (ICLR 2021) Oral Presentation [top: 1.8%] Chenlin Meng, Jiaming Song, Yang Song, Shengjia Zhao, and Stefano Ermon [Paper | Project Page | Code]
- Denoising Diffusion Implicit Models (ICLR 2021) Jiaming Song, Chenlin Meng and Stefano Ermon [Paper | Code]
- Autoregressive Score Matching (NeurIPS 2020) Chenlin Meng, Lantao Yu, Yang Song, Jiaming Song and Stefano Ermon [ Paper | Code ]
- Gaussianization Flows (AISTATS 2020) Chenlin Meng, Yang Song, Jiaming Song and Stefano Ermon [ Paper | Code ]
- MintNet: Building Invertible Neural Networks with Masked Convolutions (NeurIPS 2019) Yang Song*, Chenlin Meng*, and Stefano Ermon [ Paper | Code ]
- Learning to Interpret Satellite Images in Global Scale Using Wikipedia (IJCAI 2019) Burak Uzkent, Evan Sheehan, Chenlin Meng, Zhongyi Tang, Marshall Burke, David Lobell, and Stefano Ermon [ Paper | Code]
- Predicting Economic Development using Geolocated Wikipedia Articles (KDD 2019) Evan Sheehan*, Chenlin Meng*, Matthew Tan, Burak Uzkent, Neal Jean, Marshall Burke, David Lobell, and Stefano Ermon [ Paper | Code]
Selected Computer Graphics Projects
-
Rendering Cotton Candy on the Cup

Grand prize winning project for the 2018 Rendering Competition. Modeled and built the scene Cotton Candy on the Cup in PBRT, a computer graphics rendering system. All the models in the scene are built from scratch. Composed the final scene and tuned the final image.
-
Rendering and Building the Beauty and the Beast scene

Modeled and rendered the 3D scene Beauty and the Beast in the given ray tracer. Built and textured all the 3D models (e.g. violin, rose, cloth, books, water, etc) from scratch. Composed the final scene and tuned the final image.
-
Hair Simulation in Blender

Modeled and simulated hair motion in Blender.
Professional Services
- Journal reviewer:
JMLR, TMLR - Conference reviwer:
ICLR, NeurIPS, ICML,AISTATS, UAI, CVPR, ICCV, ECCV, ACM SIGGRAPH
Selected Coursework
- Math Courses:
Differential Topology, Galois Theory, Combinatorics, Graph Theory, Abstract Algebra, Number Theory, Complex Analysis, Analysis on Manifolds, Mathematical Analysis, Discrete Mathematics, Numerical Analysis.
-
CS Courses:
Computer Graphics, Machine Learning, Deep Learning, Analysis of Algorithms, Computer System.
Honors and Awards
- Stanford Interdisciplinary Graduate Fellowship, 2022
- Cadence Women in Technology Scholarship, 2022
- Stanford CS348B Rendering Competition, 2018: Grand Prize
Personal
I am a fan of arts and 3D animation. I also love music, especially movie soundtracks.
